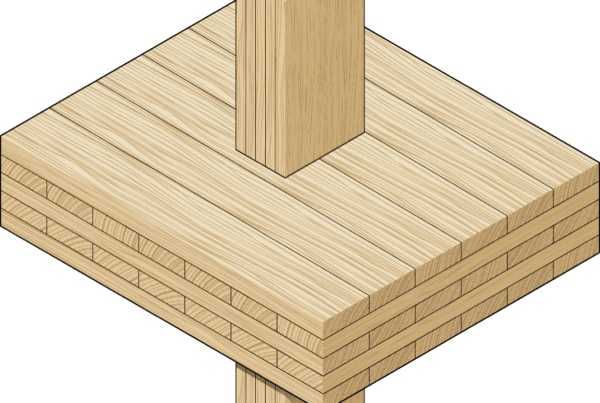
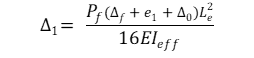Brettsperrholzwände (Cross-Laminated Timber, CLT) sind Holzwerkstoffplatten, die aus mehreren kreuzweise angeordneten und miteinander verleimten Holzbrettern bestehen. CLT-Wände weisen im Vergleich zu herkömmlichen Holzkonstruktionen eine hohe vertikale Tragfähigkeit auf und ermöglichen den Bau hoher Holzgebäude, die sonst nicht realisierbar wären.
CLT-Wandverkleidung:
Der Begriff "Rahmen" bezieht sich auf das strukturelle System, das die CLT-Paneele trägt und sowohl Stabilität als auch Tragfähigkeit gewährleistet. Dieses System besteht aus verschiedenen Komponenten, die so konzipiert sind, dass sie zusammen funktionieren und die strukturelle Integrität der Wand aufrechterhalten. Die Auswahl eines geeigneten Rahmensystems hängt von Faktoren wie der Gebäudehöhe, architektonischen Vorlieben, örtlichen Bauvorschriften und bautechnischen Anforderungen ab.
Die Einrahmung kann in die folgenden Typen eingeteilt werden:
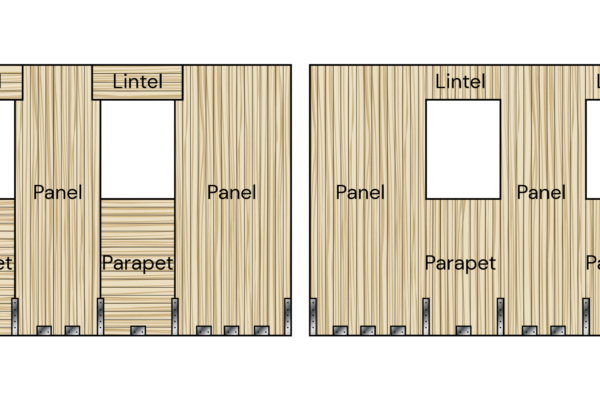
Plattform-Typ:
Referenz: CLT-Handbuch-Kanada:2019
Bei diesem System dient die Bodenplatte eines jeden Stockwerks als Basis für die Errichtung der CLT-Wände des nächsten Stockwerks. Folglich entspricht die Höhe der CLT-Wände der Geschosshöhe. Auf jeder Ebene übertragen die CLT-Wände die Schwerkraftlasten aus dem darüber liegenden Geschoss auf die darunter liegenden CLT-Bodenplatten. Da sich die Schwerkraftlasten in der Struktur nach unten hin akkumulieren, wird die Gesamthöhe des Gebäudes häufig durch den Druckwiderstand der CLT-Bodenplatten auf der untersten Ebene senkrecht zur Faser begrenzt. Diese Bauweise umfasst jedoch in der Regel eine große Anzahl von Wänden, die auch zum Widerstand gegen seismische Belastungen beitragen können und ein hohes Maß an Redundanz bieten.
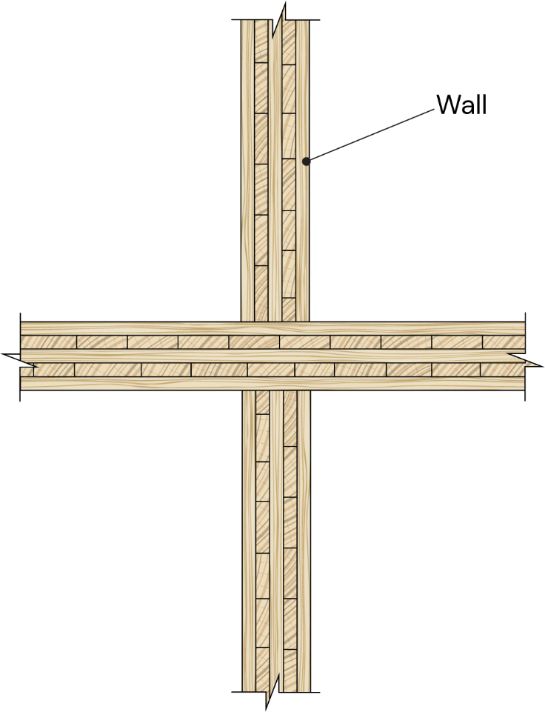
Abbildung 1: CLT-Wand mit Plattformrahmen
Ballon-Typ:
Referenz: CLT-Handbuch-Kanada:2019
Bei ballonartigen CLT-Strukturen erstrecken sich die CLT-Wände durchgehend über die gesamte Höhe des Gebäudes, wobei die Bodenplatten in jedem Stockwerk angebracht (oder aufgehängt) sind. Bei dieser Konfiguration besteht das Querlastsicherungssystem (LLRS) in der Regel aus einer geringeren Anzahl von Wänden innerhalb des Grundrisses.
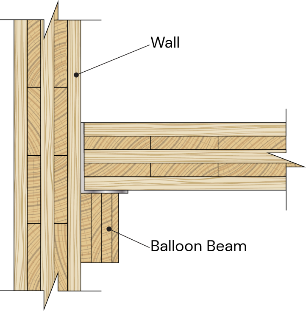
Abbildung 2: CLT-Wand mit Ballonrahmen
CLT-Wandexzentrizitäten
Perfekt zentrierte Axiallasten in Wänden sind selten, da typischerweise ein Moment durch die Exzentrizität der aufgebrachten Axiallasten, die Belastung außerhalb der Ebene oder beides zusammen entsteht. Dieses Moment führt zu einer Durchbiegung außerhalb der Ebene, ∆. Folglich wirkt die aufgebrachte Axiallast auf diese abgelenkte Form und erzeugt aufgrund des P∆-Effekts ein zusätzliches Moment. Quellen für eine Biegung außerhalb der Ebene können exzentrisch aufgebrachte Axiallasten (aufgrund von Querschnittsverlusten durch Feuer, unsymmetrischem Aufbau oder anderen Faktoren) und Windkräfte außerhalb der Ebene sein.
Umgang mit CLT-Wandexzentrizitäten mit der CLT Toolbox
Der CLT Toolbox Wall Calculator ist ein hochentwickeltes Werkzeug mit einer Vielzahl von Möglichkeiten. Eine seiner Hauptfunktionen ist die Bestimmung der Exzentrizitäten einer CLT-Wand anhand von vier Methoden: der CSA 086:19-Methode, der USA CLT Handbook-Methode, der manuellen Eingabe und der Revised Eurocode 23-Methode. Jeder Ansatz beginnt mit der Exzentrizitätsberechnung erster Ordnung, gefolgt von der Exzentrizitätsberechnung zweiter Ordnung, die nach den vier Methoden durchgeführt wird. Das Tool berechnet schließlich die Gesamtexzentrizität, die dann in der Wandanalyse verwendet wird.
Exzentrizität erster Ordnung
Bei der Analyse von Wänden ist es von entscheidender Bedeutung, verschiedene Quellen der Exzentrizität erster Ordnung zu berücksichtigen, einschließlich der Exzentrizität der von oben einwirkenden Axiallasten (ep), der Exzentrizität aufgrund von axialen Ballonlasten (eb), der Exzentrizität aufgrund von Verschiebungen der neutralen Achse, Belastungen außerhalb der Ebene und anfänglichen geometrischen Mängeln der Wand.
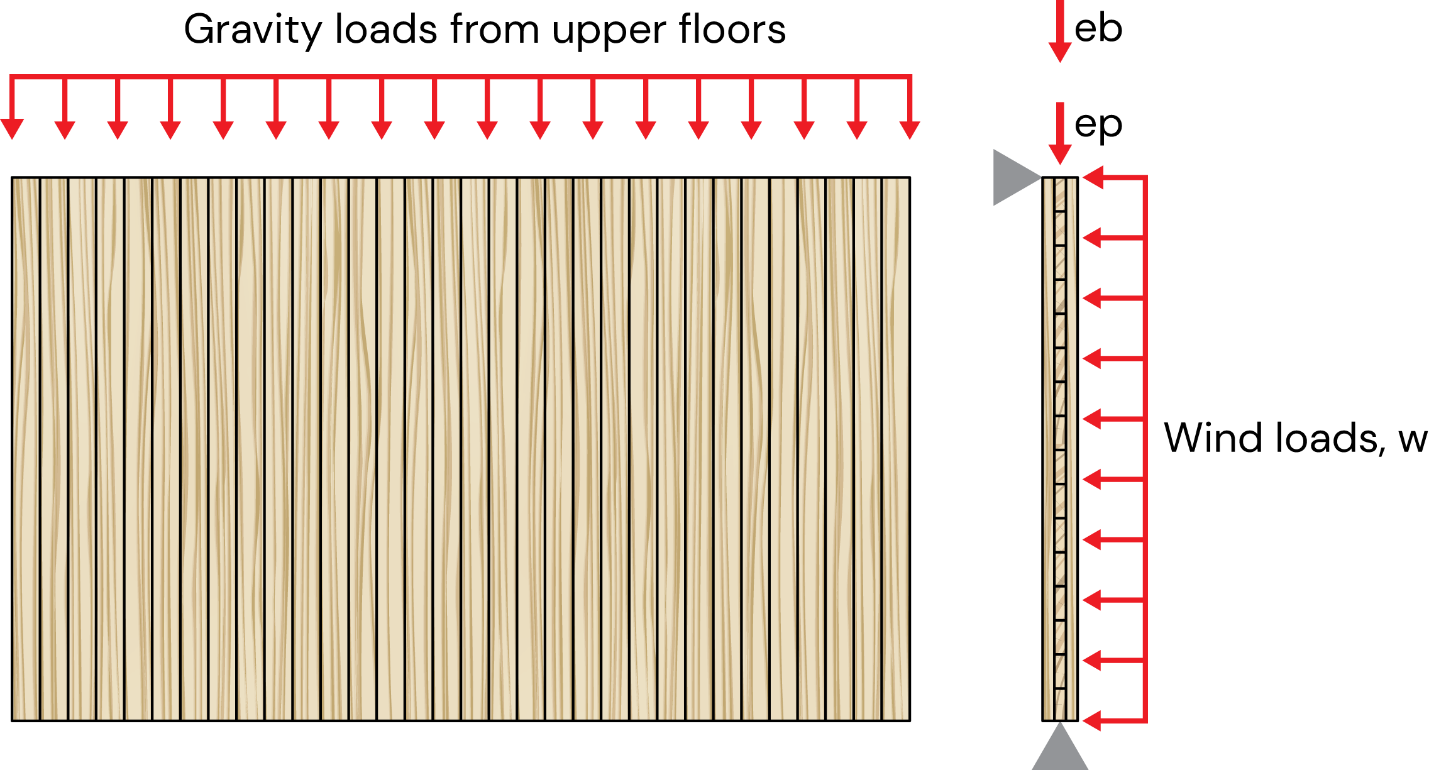
Abbildung 3: Lastverteilung auf eine CLT-Wand
1. Neutrale Achsenverschiebung, eo
Bei Umgebungsbedingungen, bei denen CLT-Elemente in der Regel einen symmetrischen (ausgewogenen) Aufbau haben, bleibt die neutrale Achse in der geometrischen Mitte. Wenn der Aufbau jedoch asymmetrisch ist, verschiebt sich die neutrale Achse vom geometrischen Mittelpunkt weg. Im Falle eines Brandes wird der Querschnitt durch die Verkohlung immer kleiner, wodurch ein asymmetrischer (unausgewogener) Aufbau entsteht. Infolgedessen verschiebt sich die neutrale Achse zu der Seite, die der Brandeinwirkung gegenüberliegt.
![]()
Wobei:
tp =Dicke der Wand
yc= Lage der neutralen Achse
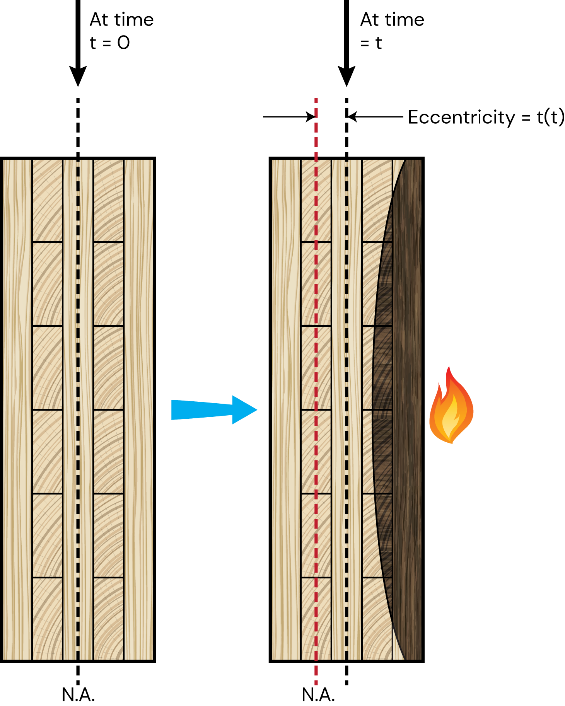
Abbildung 4: CLT-Wandelement unter kombinierter Biege- und Axialdruckbeanspruchung
Der Abstand von der Axiallast zur neutralen Achse (maßgebend für die Exzentrizität) kann wie folgt ermittelt werden:
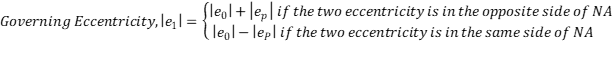
Wobei:
eo= Verschiebung der neutralen Achse
ep= tatsächliche Exzentrizität der Last aus der Axiallast oben
Der Abstand der Axiallast vom Ballonträger zur neutralen Achse (maßgebliche Exzentrizität) kann wie folgt ermittelt werden:
Wobei:
eo= Verschiebung der neutralen Achse
eb= tatsächliche Lastexzentrizität aus der axialen Ballonlast
2. Durchbiegung bei Windbelastung außerhalb der Ebene
Die Durchbiegung (Δ) einer CLT-Bodenplatte mit der Länge l, die einer gleichmäßig verteilten Last w ausgesetzt ist, kann mit verschiedenen analytischen Methoden bestimmt werden.
Wenn die analytische Methode die Scheranalogiemethode ist: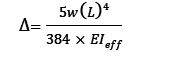
Wenn die Analysemethode Gamma oder Extended Gamma ist:
Wenn die analytische Methode Timoshenko ist:
Dabei ist EI die Biegesteifigkeit auf der Grundlage der spezifischen Methode.
3.Anfängliche geometrische Unvollkommenheiten der Wand
Anfängliche Imperfektionen sind bei der Planung von Wänden von entscheidender Bedeutung. In der Statik beziehen sich Imperfektionen auf Abweichungen und Unstimmigkeiten, die sich aus Faktoren wie Fertigungstoleranzen, Materialschwankungen und Konstruktionsfehlern ergeben. Diese Unvollkommenheiten führen dazu, dass reale Strukturen von einem "idealen" oder theoretisch perfekten Zustand abweichen, was sich auf ihre Leistung unter einwirkenden Lasten auswirken kann.
Gemäß CSA 086;19
CLT-Handbuch-Kanada:2019, Abschnitt 3.10.4
anfängliche Wandunvollkommenheiten in der Mitte der Platte, in der Regel als L/500 + h/6, wobei L die Plattenhöhe und h die Anfangstiefe der Platte in mm ist .
Laut USA CLT-Handbuch
Mit dem CLT-Wandrechner der CLT-Toolbox können Benutzer die anfänglichen Wandimperfektionen manuell eingeben, da das Handbuch keine Formel für die Berechnung vorsieht.
Gemäß dem revidierten Eurocode 23
Bezug: prEN 1995-1-1:2023, Abschnitt 7.3.1
Die äquivalente Bogenunvollkommenheit (e) sollte mindestens wie folgt berücksichtigt werden:

Dabei ist l die Höhe der Mauer.
Exzentrizität zweiter Ordnung
Effekte zweiter Ordnung, die auch als P-Delta-Effekte bezeichnet werden, treten auf, wenn eine exzentrische Axialkraft (z. B. Eigengewicht oder eine aufgebrachte Last) in Kombination mit axialen und horizontalen Lasten ein Biegemoment und zusätzliche Verschiebungen erzeugt. Bei einem CLT-Wandaufbau können diese Effekte (P-Δ-Effekte) auch durch die Verkohlung der brandexponierten Oberfläche entstehen, die den Querschnitt verringert und die strukturelle Stabilität der Wand beeinträchtigt.
Gemäß CSA 086;19
CLT-Handbuch-Kanada:2019, Abschnitt 3.10.4
Mit der folgenden Formel wird die Exzentrizität zweiter Ordnung berechnet:
A) für die Einrahmung von Ballons
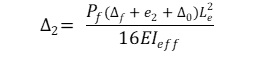
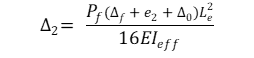
wobei:
Δf = Durchbiegung aufgrund einer Belastung außerhalb der Ebene (Biegung), in mm
e1 = maßgebliche Exzentrizität der Axiallast, in mm
e2 =Richtige Exzentrizität der Axiallast vom Ballonträger, in mm
Δ₀ = Anfängliche Wandunvollkommenheiten in halber Höhe der Platte, typischerweise L/500 + h/6, wobei:
L = Plattenhöhe, in mm
h = Anfangstiefe der Platte, in mm
B) für Plattformrahmen
Laut USA CLT-Handbuch
CLT-Handbuch-USA:2013, Kapitel-8, Abschnitt 4.1.9
Mit der folgenden Formel wird die Exzentrizität zweiter Ordnung berechnet:
A) für die Einrahmung von Ballons
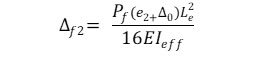
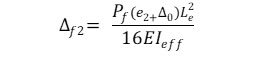
Wobei:
e1 =Richtige Exzentrizität der Axiallast, in mm
e2 = maßgebende Exzentrizität der Axiallast vom Ballonträger, in mm
Δ₀ = anfängliche Wandunvollkommenheiten aus Benutzereingaben
Gesamtexzentrizität:
![]()
![]()
Wobei:
e1 =Richtige Exzentrizität der Axiallast, in mm
e2 = maßgebende Exzentrizität der Axiallast vom Ballonträger, in mm
Δ₀ = Anfängliche Wandunvollkommenheiten aus Benutzereingaben
Δw= Durchbiegung aufgrund der Belastung außerhalb der Ebene (Biegung), in mm
B) für Plattformrahmen
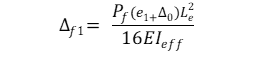
Exzentrizität insgesamt:
Gemäß dem revidierten Eurocode 23
Bezug: prEN 1995-1-1:2023, Abschnitt 7.4.2
Für einen Stab, der einer äquivalenten Biegefehlstelle ez oder ey mit einer konstanten Bemessungsdruckkraft 𝑁Ed und einem einachsigen Bemessungsbiegemoment um die y- oder z-Achse, das nichtlineare Bemessungsmoment ![]() um die jeweilige Achse kann wie folgt bestimmt werden:
um die jeweilige Achse kann wie folgt bestimmt werden:
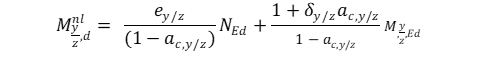
Mit:
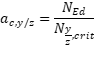
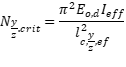
Wobei:
αc, y/zist der Verstärkungsfaktor für kritische Normalkräfte;
δy/zder Dischinger-Koeffizient unter Berücksichtigung der jeweiligen Verteilung von entwederMy, Ed oder Mz,Ed ist;
Ny/z, ist die kritische Kraft für das Biegeknicken um die jeweilige Achse.
E0, d ist der Bemessungs-Elastizitätsmodul parallel zur Faser;
I y/z ist das zweite Trägheitsmoment um die y- bzw. z-Achse;
ly/z, ef ist die effektive gestauchte Länge.
Darüber hinaus werden im CLTTOOLBOX-Wandrechner die Momentenberechnungen für jede Methode getrennt durchgeführt, wobei die jeweilige Exzentrizität berücksichtigt wird.
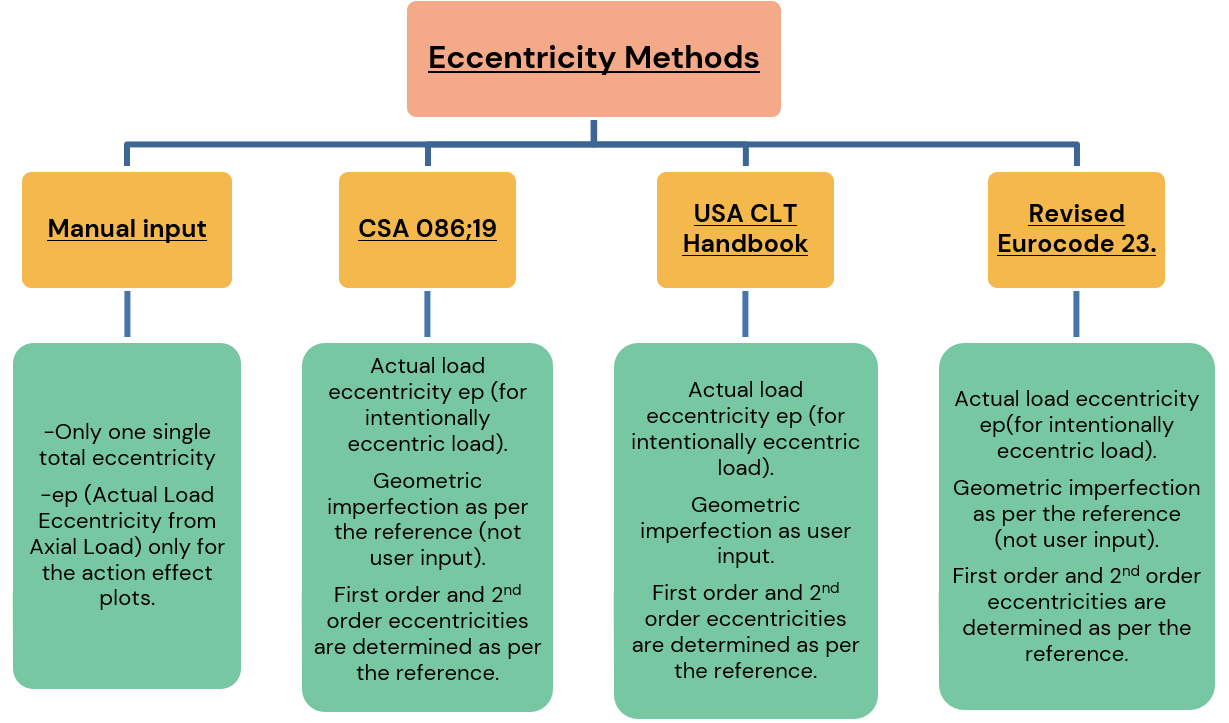
Abbildung 5: Überlegungen zur Exzentrizität einer CLT-Wand in Plattformbauweise
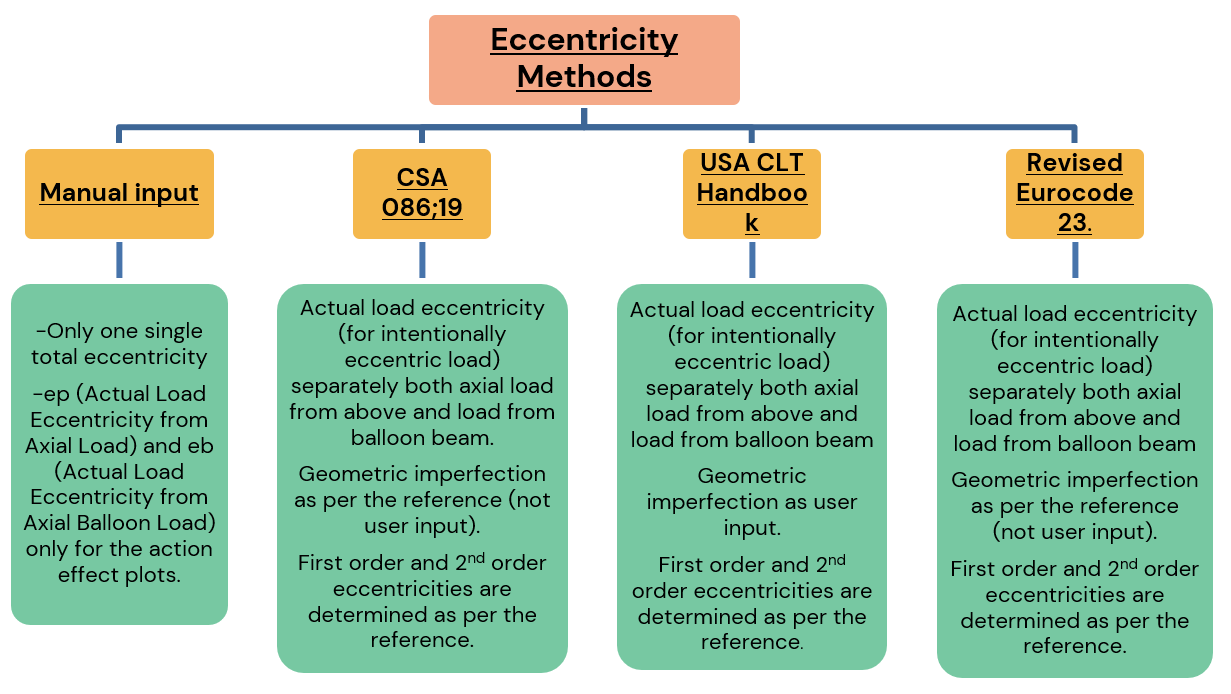
Abbildung 6: Überlegungen zur Exzentrizität einer CLT-Wand in Ballonbauweise