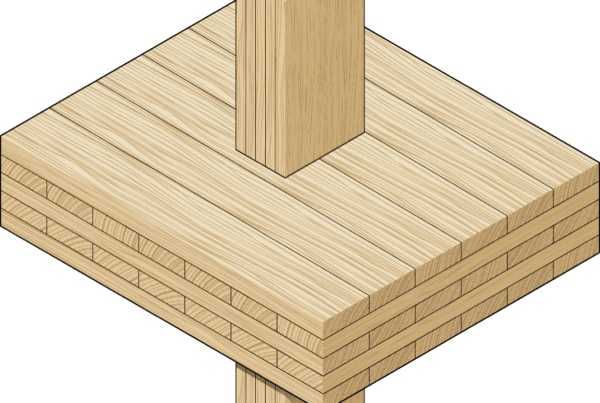
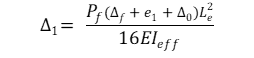Los muros de madera contralaminada (CLT) son paneles de madera compuestos por varias capas de tablas de madera dispuestas transversalmente y unidas entre sí. Los muros de CLT presentan una gran capacidad de carga vertical en comparación con las estructuras de madera convencionales, lo que permite construir edificios altos de madera que de otro modo serían inviables.
Armazón de pared CLT:
Por armazón se entiende el sistema estructural que soporta los paneles CLT, garantizando tanto la estabilidad como la capacidad de carga. Este sistema se compone de diversos componentes diseñados para funcionar conjuntamente, manteniendo la integridad estructural del muro. La selección de un sistema de entramado adecuado depende de factores como la altura del edificio, las preferencias arquitectónicas, los códigos de construcción locales y los requisitos de ingeniería estructural.
El encuadramiento puede clasificarse en los siguientes tipos:
Tipo de plataforma:
Referencia: Manual CLT-Canadá:2019
En este sistema, la plataforma de cada piso sirve de base para levantar los muros de CLT del piso siguiente. Como resultado, la altura de los muros de CLT se corresponde con la altura del piso. En cada nivel, los muros de CLT transfieren las cargas gravitatorias del piso superior a los paneles de CLT del piso inferior. Dado que las cargas gravitatorias se acumulan en la estructura, la altura total del edificio suele estar limitada por la resistencia a la compresión perpendicular a la fibra de los paneles del suelo de CLT en el nivel más bajo. Sin embargo, este método de construcción suele incorporar un gran número de muros, que también pueden contribuir a la resistencia a las cargas sísmicas, proporcionando un alto grado de redundancia.
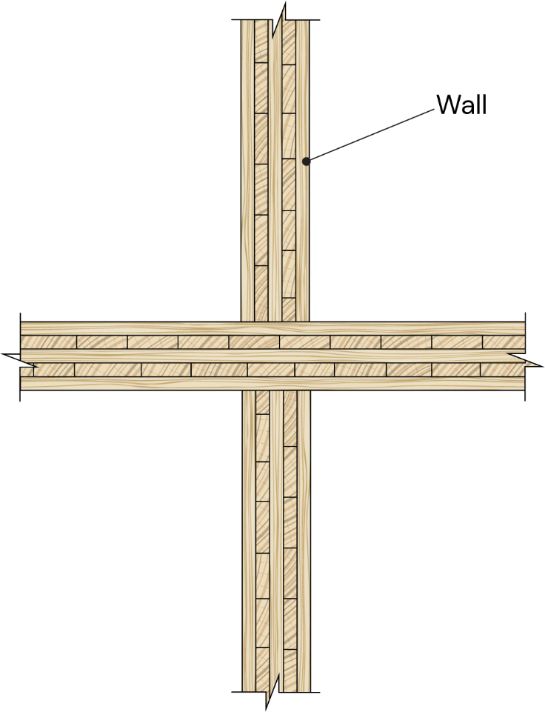
Figura 1: Muro de CLT con armazón de plataforma
Tipo de globo:
Referencia: Manual CLT-Canadá:2019
En las estructuras CLT tipo globo, los muros CLT se extienden de forma continua a lo largo de toda la altura del edificio, con paneles de suelo fijados (o suspendidos) en cada planta. En esta configuración, el sistema de resistencia a cargas laterales (LLRS) suele consistir en un menor número de muros dentro de la planta.
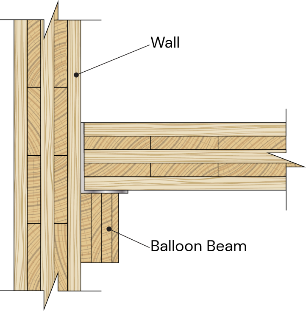
Figura 2: Muro de CLT con entramado balón
Excentricidades del muro CLT
La carga axial perfectamente centrada en los muros es poco frecuente, ya que suele producirse un momento debido a la excentricidad de las cargas axiales aplicadas, a la carga fuera del plano o a ambas combinadas. Este momento provoca una flexión fuera del plano, ∆. En consecuencia, la carga axial aplicada actúa sobre esta forma desviada, generando un momento adicional debido al efecto P∆. Las fuentes de flexión fuera del plano pueden incluir cargas axiales aplicadas excéntricamente (debido a pérdida de sección por incendio, disposición asimétrica u otros factores) y fuerzas de viento fuera del plano.
Cómo tratar las excentricidades de los muros de CLT con CLT Toolbox
La calculadora de muros CLT Toolbox es una sofisticada herramienta con una amplia gama de funciones. Una de sus funciones principales es determinar las excentricidades de un muro CLT utilizando cuatro métodos: el método CSA 086:19, el método del Manual CLT de EE.UU., la entrada manual y el método del Eurocódigo 23 revisado. Cada enfoque comienza con el cálculo de la excentricidad de primer orden, seguido del cálculo de la excentricidad de segundo orden, que se realiza según los cuatro métodos. Finalmente, la herramienta calcula la excentricidad total, que se utiliza en el análisis del muro.
Excentricidad de primer orden
En el análisis de muros, es crucial considerar varias fuentes de excentricidad de primer orden, incluyendo la excentricidad de las cargas axiales aplicadas desde arriba (ep), la excentricidad debida a las cargas axiales del globo (eb), la excentricidad causada por los desplazamientos del eje neutro, las cargas fuera del plano y las imperfecciones geométricas iniciales del muro.
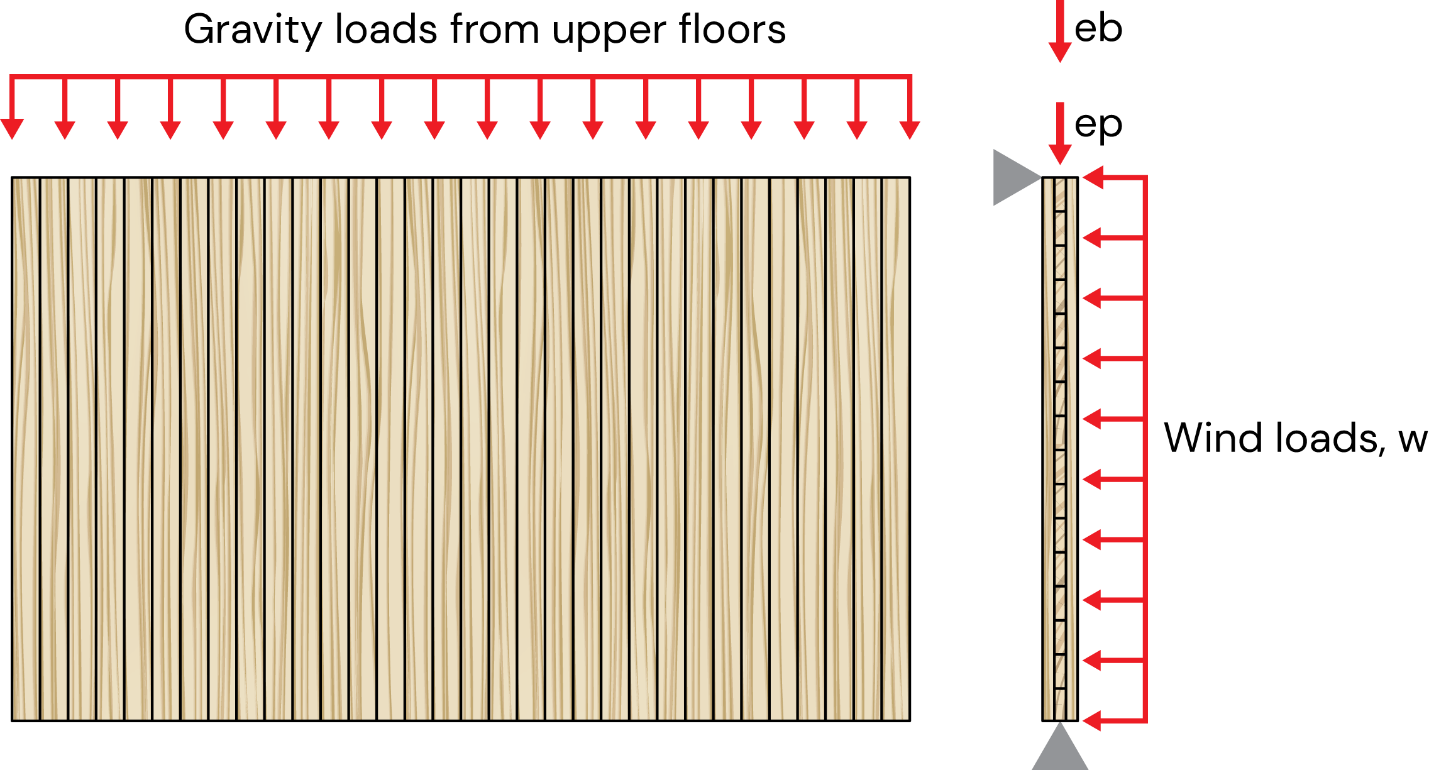
Figura 3: Distribución de la carga en un muro de CLT
1. Desplazamiento del eje neutro, eo
En condiciones ambientales, cuando los elementos CLT suelen tener una disposición simétrica (equilibrada), el eje neutro permanece en el centro geométrico. Sin embargo, si la composición es asimétrica, el eje neutro se desplaza del centro geométrico. En caso de incendio, la carbonización reduce progresivamente la sección transversal, creando una disposición asimétrica (desequilibrada). Como resultado, el eje neutro se desplaza hacia el lado opuesto a la exposición al fuego.
![]()
Donde
tp = Espesor del muro
yc= Localización del eje neutro
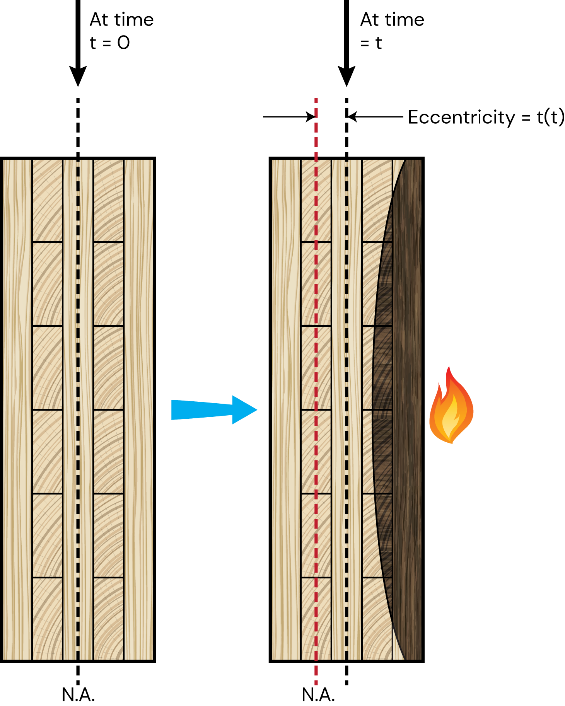
Figura 4: Elemento de muro de CLT sometido a flexión y compresión axial combinadas
La distancia de la carga axial al eje neutro (que rige la excentricidad ) se puede hallar de la siguiente manera:
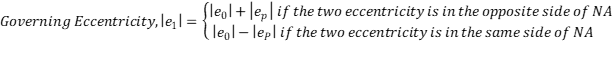
Donde:
eo=desplazamiento del eje neutro
ep=excentricidad de la carga axial superior
La distancia de la carga axial de la viga globo al eje neutro (excentricidad gobernante) puede ser encontrada como sigue:
Donde:
eo= desplazamiento del eje neutro
eb= excentricidad real de la carga del globo axial
2. desviación de la carga de viento fuera del plano
La deflexión (Δ) de un panel de suelo CLT con longitud l, sometido a una carga uniformemente distribuida w, puede determinarse utilizando diferentes métodos analíticos.
Si el método analítico es el método de analogía de cizalla: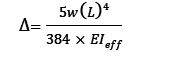
Si el método analítico es Gamma o Gamma Extendido:
Si el método analítico es Timoshenko:
Donde EI es la rigidez a la flexión basada en el método específico.
3.Imperfecciones geométricas iniciales del muro
Las imperfecciones iniciales son consideraciones cruciales en el diseño de muros. En el análisis estructural, las imperfecciones se refieren a las desviaciones e incoherencias derivadas de factores como las tolerancias de fabricación, la variabilidad de los materiales y las imprecisiones en la construcción. Estas imperfecciones hacen que las estructuras reales se desvíen de una condición "ideal" o teóricamente perfecta, influyendo potencialmente en su comportamiento bajo las cargas aplicadas.
Según CSA 086;19
Manual CLT-Canadá:2019, sección 3.10.4
imperfecciones iniciales de la pared a media altura del panel, normalmente tomadas como L/500 + h/6, siendo L la altura del panel y h la profundidad inicial del panel, en mm.
Según el Manual CLT de EE.UU.
La calculadora de muros CLT de CLT Toolbox permite a los usuarios introducir manualmente las imperfecciones iniciales del muro, ya que el Manual no proporciona una fórmula para el cálculo.
Según el Eurocódigo 23 revisado
Referencia: prEN 1995-1-1:2023, Sección 7.3.1
La imperfección de arco equivalente (e) debe considerarse, como mínimo, de la siguiente manera:

Donde l es la altura del Muro.
Excentricidad de segundo orden
Los efectos de segundo orden, también denominados efectos P-delta, se producen cuando una fuerza axial excéntrica (como el peso propio o una carga aplicada), en combinación con cargas axiales y horizontales, genera un momento flector y un desplazamiento adicional. En un conjunto de muro CLT, estos efectos (efectos P-Δ) también pueden desarrollarse debido a la carbonización de la superficie expuesta al fuego, lo que reduce la sección transversal e impacta en la estabilidad estructural del muro.
Según CSA 086;19
Manual CLT-Canadá:2019, Sección 3.10.4
La siguiente fórmula calcula la excentricidad de segundo orden:
A) para enmarcar globos
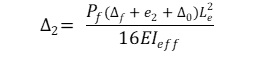
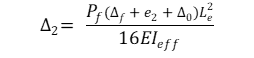
Donde:
Δf = Deflexión debida a la carga fuera del plano (flexión), en mm.
e1 = Excentricidad determinante de la carga axial, en mm
e2 = Excentricidad gobernante de la carga axial de la viga balón, en mm
Δ₀ = Imperfecciones iniciales de la pared a media altura del panel, normalmente tomadas como L/500 + h/6, donde:
L = Altura del panel, en mm
h = Profundidad inicial del panel, en mm
B) para el armazón de la plataforma
Según el Manual CLT de EE.UU.
CLT Handbook-USA:2013, Capítulo-8,Sección 4.1.9
La siguiente fórmula calcula la excentricidad de segundo orden:
A) para enmarcar globos
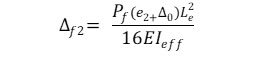
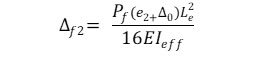
Donde
e1 = Excentricidad determinante de la carga axial, en mm
e2 =Excentricidad gobernante de la carga axial de la viga balón, en mm
Δ₀ = Imperfecciones iniciales de la pared a partir de la entrada del usuario
Excentricidad total:
![]()
![]()
Donde
e1 = Excentricidad determinante de la carga axial, en mm
e2 =Excentricidad gobernante de la carga axial de la viga balón, en mm
Δ₀ = Imperfecciones iniciales de la pared a partir de la entrada del usuario
Δw= Desviación debida a la carga fuera del plano (flexión), en mm
B) para el armazón de la plataforma
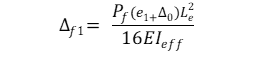
Excentricidad total:
Según el Eurocódigo 23 revisado
Referencia: prEN 1995-1-1:2023, Sección 7.4.2
Para un elemento sometido a una imperfección de arco equivalente ez o ey con una fuerza de compresión de diseño constante 𝑁Ed y un momento flector de cálculo uniaxial aplicado alrededor de los ejes y o z, el momento no lineal de cálculo ![]() alrededor del eje respectivo puede determinarse como sigue:
alrededor del eje respectivo puede determinarse como sigue:
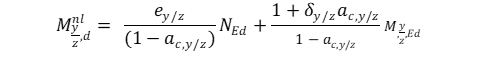
Con:
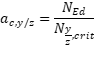
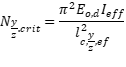
Donde:
αc,y/zes el factor de amplificación de las fuerzas normales críticas;
δy/zes el coeficiente de Dischinger teniendo en cuenta la distribución respectiva deMy, Ed o Mz,Ed;
Ny/z, es la fuerza crítica para el pandeo por flexión alrededor del eje respectivo.
E0, d es el módulo de elasticidad de cálculo paralelo a la fibra;
I y/z es el segundo momento de inercia alrededor del eje y o z, respectivamente;
ly/z, ef es la longitud efectiva comprimida.
Además, en la calculadora de muros CLTTOOLBOX, los cálculos de momento se realizan por separado para cada método, considerando la excentricidad respectiva.
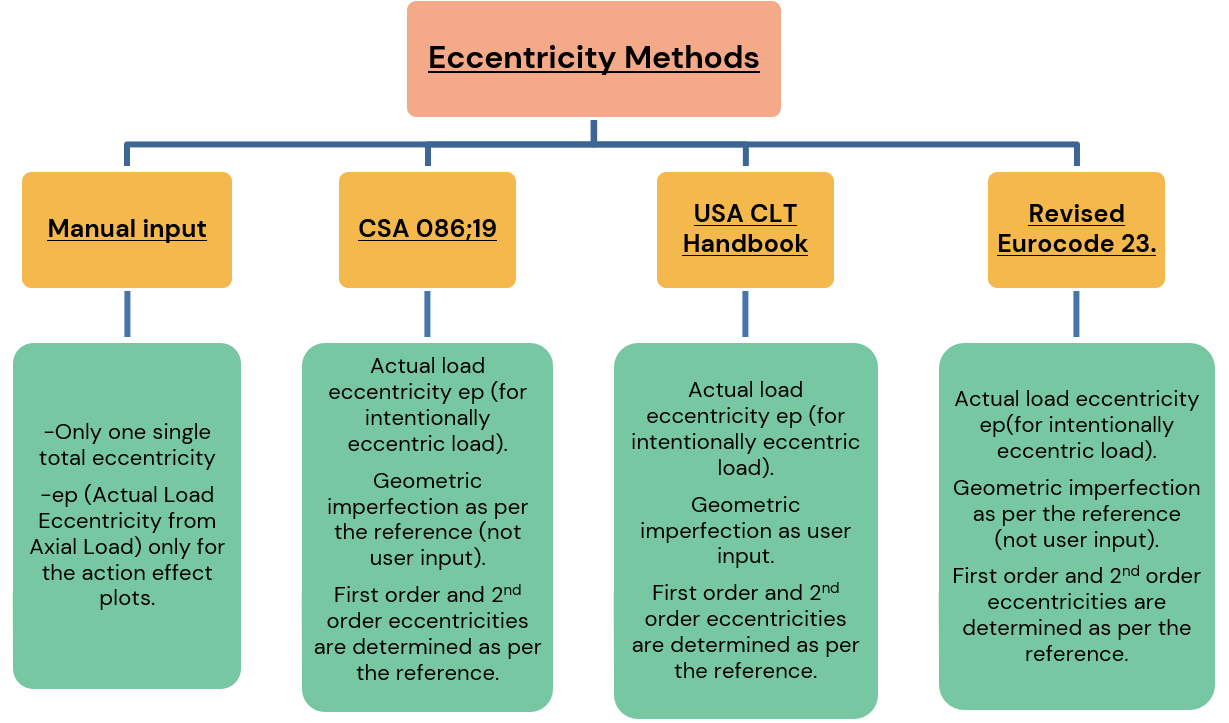
Figura 5: Consideraciones de excentricidad para el muro CLT tipo plataforma
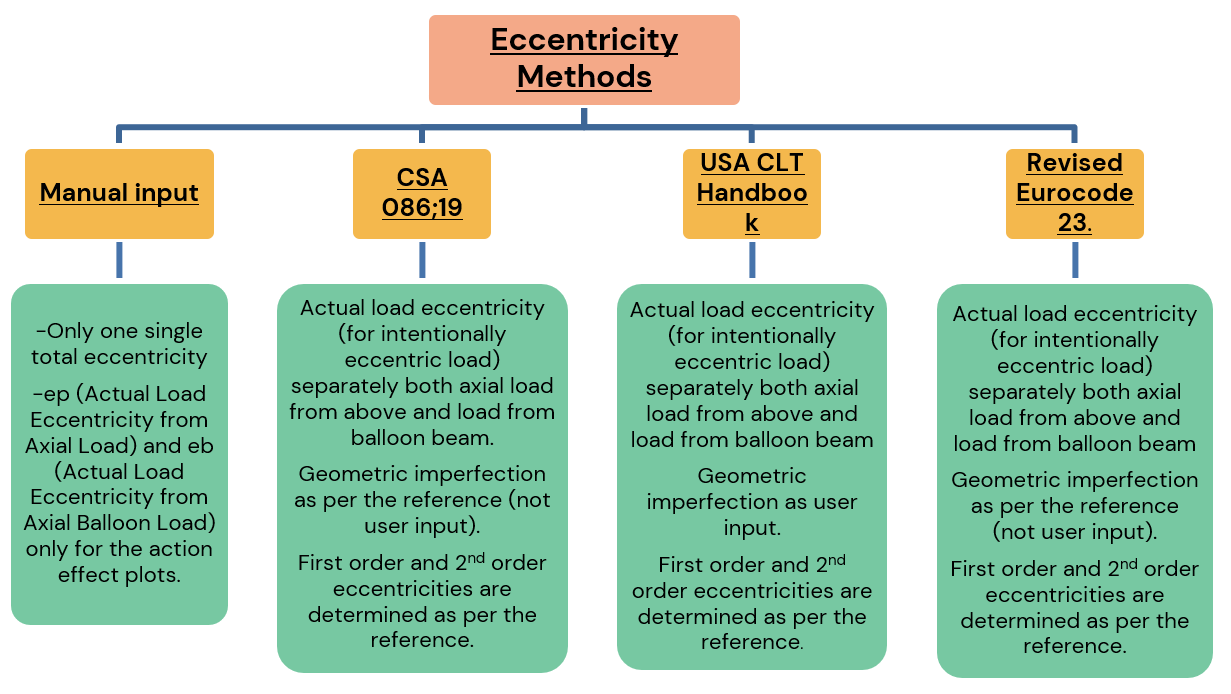
Figura 6: Consideraciones sobre la excentricidad del muro CLT tipo globo